【前言】
楼主只是一个刚开始研究算法没多久的小萌新，本帖主要用于记录LeetCode网站刷题的实况，遇到的一些个人认为值得分享的题目。本帖问题的代码实现部分将采用Java语言。由于个人能力和水平的有限，本帖内容不能保证100%准确和算法最优解，所有代码与思路仅供参考。欢迎各位大佬和计算机爱好者参与讨论并提出问题与指正！
【题目描述】
5. 最长回文子串
难度：中等
给你一个字符串 s，找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。
【示例与提示】
示例 1：
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。
示例 2：
输入：s = "cbbd"
输出："bb"
提示：
1 <= s.length <= 1000
s 仅由数字和英文字母组成
【实现思路】
这个题目可以尝试采取动态规划的方式解决问题，具体的思路如下：
1.首先，创建一个动态规划表，表的类型为行数、列数均为提供字符串s的长度的一个布尔型（boolean）二维数组isPalindrome，当isPalindrome[i][j]为true时，代表s从i到j（包含i和j）的字串是一个回文串，否则不是。当isPalindrome的全部元素（其实也不是，在这里只有i ≤ j的部分是有意义的）按照s所含回文字串的情况更新一致后，就能够通过找到满足isPalindrome[i][j]为true、并且(j - i)最大的i和j的值，此时s从i到j的字串就是符合题意的字串。
2.isPalindrome为true的条件可以分类讨论，如下：
·当s[i]（表示字符串s中下标为i的字符）与s[j]不相等时，即这个字串的头尾不相等，显然不是字串，isPalindrome[i][j]为false。
·当s[i]与s[j]相等时，又可以分为如下三个情况讨论：
①当i = j时，s从i到j的字串，即下标为i的单个字符，显然符合回文串的定义，isPalindrome[i][j]为true。
②当j - i = 1时，字串为相邻且相等的两个字符（如"aa"），显然也符合回文串的定义，isPalindrome[i][j]为true。
③其他情况，即i与j不相邻时，仅当isPalindrome[i + 1][j - 1]为true，isPalindrome[i][j]为true才成立。例如：字符串"axxxa"如果是一个回文串，则"xxx"必须是个回文串。
3.关于isPalindrome数组的初始化，直接使用默认值false，这样当s[i]与s[j]不相等时，不用作任何处理即可
4.isPalindrome数组的遍历：
在关于什么时候isPalindrome[i][j]值为true的分析中，不难发现在i和j不相邻的情况下，isPalindrome[i + 1][j - 1]的值必须已经确定，即isPalindrome[i + 1][j - 1]必须先于isPalindrome[i][j]得到遍历。因此，在遍历时，i将采取从(s.length - 1)到0，j将采取从0到(s.length - 1)的先行后列（在操作系统的页式存储方式下，采取先行后列的遍历方式会更快）的遍历方式，即遍历行的时候是逆向，遍历列的时候是正向。
【代码实现】（java）

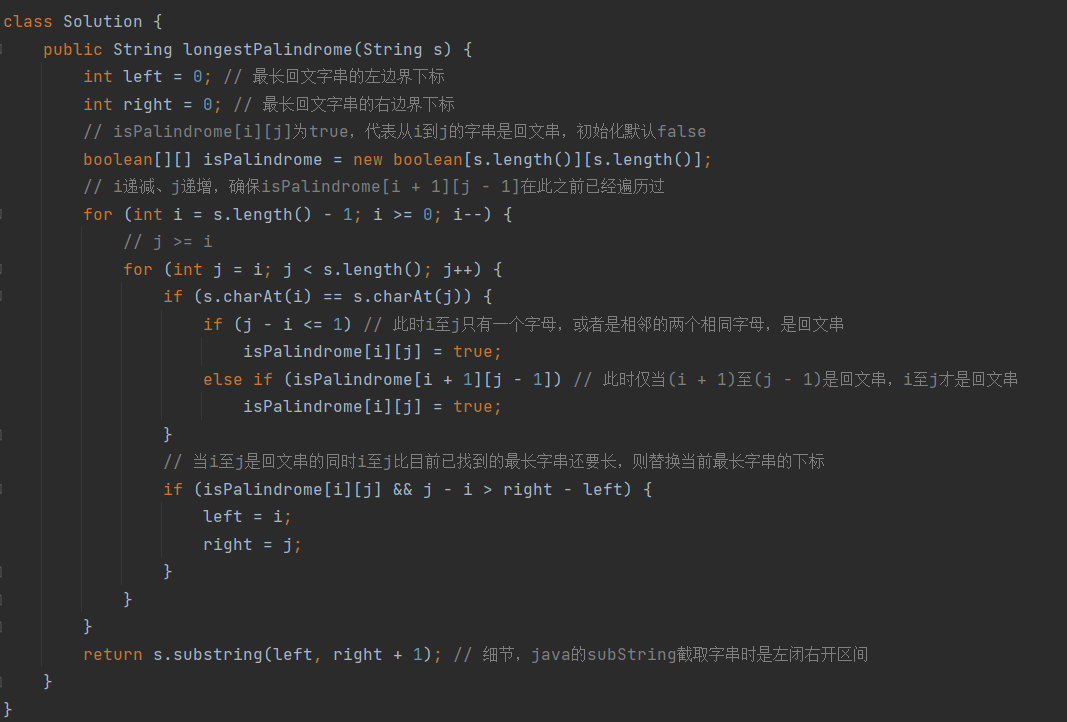
class Solution {
public String longestPalindrome(String s) {
int left = 0; // 最长回文字串的左边界下标
int right = 0; // 最长回文字串的右边界下标
// isPalindrome[i][j]为true，代表从i到j的字串是回文串，初始化默认false
boolean[][] isPalindrome = new boolean[s.length()][s.length()];
// i递减、j递增，确保isPalindrome[i + 1][j - 1]在此之前已经遍历过
for (int i = s.length() - 1; i >= 0; i--) {
// j >= i
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j)) {
if (j - i <= 1) // 此时i至j只有一个字母，或者是相邻的两个相同字母，是回文串
isPalindrome[i][j] = true;
else if (isPalindrome[i + 1][j - 1]) // 此时仅当(i + 1)至(j - 1)是回文串，i至j才是回文串
isPalindrome[i][j] = true;
}
// 当i至j是回文串的同时i至j比目前已找到的最长字串还要长，则替换当前最长字串的下标
if (isPalindrome[i][j] && j - i > right - left) {
left = i;
right = j;
}
}
}
return s.substring(left, right + 1); // 细节，java的subString截取字串时是左闭右开区间
}
}
【算法分析与运行结果】
时间复杂度：O(n²)
空间复杂度：O(n²)
运行结果：

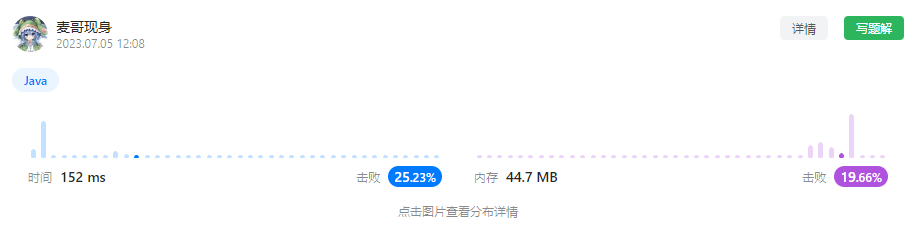
有一说一可以看出来对于这道题目来说，动态规划在时间和空间效率上都不是最优解
【进阶思路】
采取双指针法，双指针起始指向某个单个的字符、或者连续的两个字符。当这两个指针之间的部分符合回文串时，两个指针分别向左和向右延伸一个字符。如果新加入的两个字符是相等的，那么它仍然是一格回文串。一直重复延伸操作，直到某个指针已经抵达字符串的边界，或者新加入的两个字符不相等为止。遍历每个单个的字符和相邻的字符，进行延伸操作，记录最大延伸的字串长度以及左右边界的位置即可。
示例一：aabcbd，延伸从c开始
①c：是回文串，继续延伸
②bcb：是回文串，继续延伸
③abcbd：不是回文串，停止延伸，从c开始延伸的最大字符串是bcb
示例二：bccd，延伸从cc开始
①cc：是回文串，继续延伸
②bccd：不是回文串，停止延伸，从cc开始延伸的最大字符串是cc
【代码实现】（java）

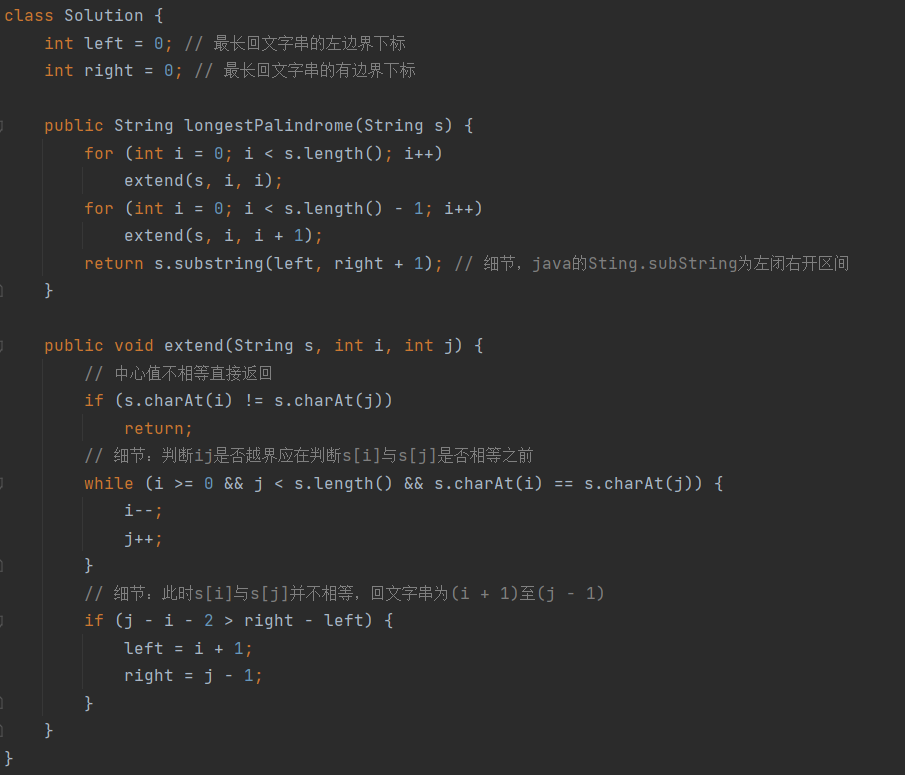
class Solution {
int left = 0; // 最长回文字串的左边界下标
int right = 0; // 最长回文字串的有边界下标
public String longestPalindrome(String s) {
for (int i = 0; i < s.length(); i++)
extend(s, i, i);
for (int i = 0; i < s.length() - 1; i++)
extend(s, i, i + 1);
return s.substring(left, right + 1); // 细节，java的Sting.subString为左闭右开区间
}
public void extend(String s, int i, int j) {
// 中心值不相等直接返回
if (s.charAt(i) != s.charAt(j))
return;
// 细节：判断ij是否越界应在判断s[i]与s[j]是否相等之前
while (i >= 0 && j < s.length() && s.charAt(i) == s.charAt(j)) {
i--;
j++;
}
// 细节：此时s[i]与s[j]并不相等，回文字串为(i + 1)至(j - 1)
if (j - i - 2 > right - left) {
left = i + 1;
right = j - 1;
}
}
}
【算法分析与运行结果】
时间复杂度：O(n²)
空间复杂度：O(1)
运行结果：

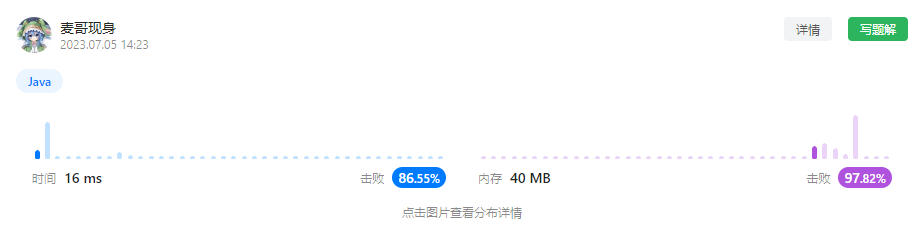
从图中可以看出，不仅时间效率得到了提升，在这个问题下双指针法常数的空间复杂度更是碾压动态规划的平方的空间复杂度。
【代码优化】
经过多次尝试，发现比通过String.charAt()来获取s的某个字符更快的方法：通过在Solution类中定义一个字符数组类型（char[]）变量chars，并在longestPalindrome()方法调用时，将s.toCharArray()赋值给chars，在此后的代码中直接通过char[i]就可以访问原字符串s的第i个字符。
尽管从算法层面而言，这多出来的O(n)的空间复杂度开销没有任何意义，像是画蛇添足，但是以实际效果，即在平台提供的测试样例的环境下看，时间效率再次得到了大幅提升。如下图所示。

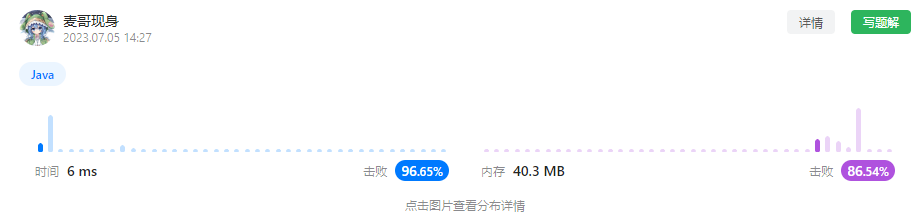
对此，我个人的分析是（不一定正确、准确）：String.charAt()方法调用、以及方法内部的判断和内部对其他方法的调用，将比直接访问一个数组的某个成员要花费更多的时间，最终影响了算法的时间效率。
【彩蛋】
下图是我在进行测试、提交代码时，发现最快的档位6ms提供的代码实例变成了我前不久刚提交的代码（可能是随机提供的，但就是很神奇）

【参考资料】
网友 “代码随想录”的评论（LeetCode题库-第5题-最长回文字串-讨论区）